1. Thế nào là khoảng cách từ một điểm đến một đường thẳng?
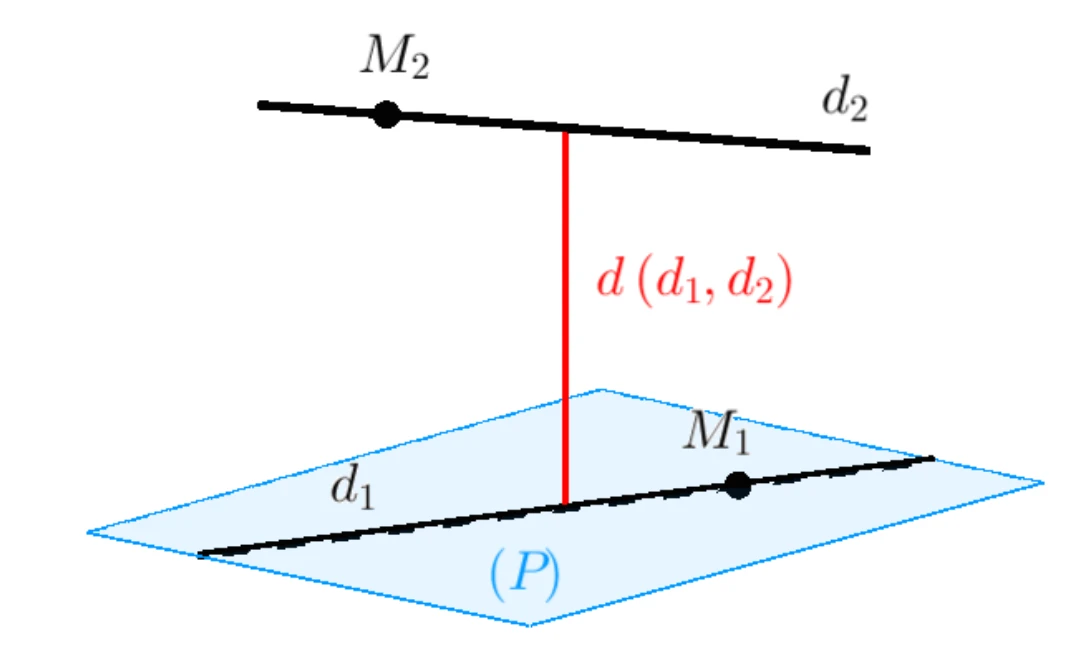
Khoảng cách từ một điểm đến một đường thẳng là một khái niệm quan trọng trong hình học và thường được ứng dụng trong nhiều bài toán thực tiễn. Để hiểu rõ hơn về khái niệm này, trước tiên chúng ta hãy xác định rõ ràng định nghĩa:
- Điểm M và đường thẳng Δ: Trong không gian 2 chiều, điểm M bất kỳ được xác định bởi tọa độ \( (x_0, y_0) \) và đường thẳng Δ có thể biểu diễn bằng phương trình tổng quát \( ax + by + c = 0 \).
- Hình chiếu H của điểm M lên đường thẳng Δ: H là điểm trên đường thẳng Δ sao cho đoạn thẳng MH vuông góc với Δ. Diện tích đoạn thẳng MH chính là khoảng cách từ điểm M tới đường thẳng Δ.

Ký hiệu:
- Kí hiệu khoảng cách \( d(M, Δ) = MH \).
Hay nói cách khác, khoảng cách từ điểm đến đường thẳng chính là độ dài của đoạn thẳng nối điểm M và hình chiếu H của nó lên đường thẳng Δ.
2. Phương pháp tính khoảng cách từ một điểm đến một đường thẳng
2.1. Công thức tính khoảng cách từ một điểm đến một đường thẳng
Để tính khoảng cách từ điểm M đến đường thẳng Δ, chúng ta có thể sử dụng công thức sau đây:
Giả sử đường thẳng Δ có phương trình như trên:
\[ Δ: ax + by + c = 0 \]
và điểm M có tọa độ \( (x_0, y_0) \), thì khoảng cách từ điểm M đến đường thẳng Δ được tính bằng công thức:
\[ d(M, Δ) = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} \]
2.2. Bài tập ví dụ tính khoảng cách từ một điểm đến một đường thẳng
Để nắm rõ hơn về phương pháp tính khoảng cách này, chúng ta hãy xem xét một số ví dụ.
Ví dụ 1: Tìm khoảng cách từ điểm \( M(1; 2) \) đến đường thẳng \( (D): 4x + 3y - 2 = 0 \).
Hướng dẫn giải:
- Áp dụng công thức tính khoảng cách, ta có:
\[ d(M, D) = \frac{|4 \times 1 + 3 \times 2 - 2|}{\sqrt{4^2 + 3^2}} = \frac{|4 + 6 - 2|}{\sqrt{16 + 9}} = \frac{8}{5} \]
Như vậy, khoảng cách từ M đến D là \( \frac{8}{5} \).
Ví dụ 2: Tính khoảng cách từ giao điểm của hai đường thẳng \( (a): x - 3y + 4 = 0 \) và \( (b): 2x + 3y - 1 = 0 \) đến đường thẳng \( Δ: 3x + y + 16 = 0 \).
Hướng dẫn giải:
- Tìm góc giao điểm A của hai đường thẳng \( (a) \) và \( (b) \) bằng cách giải hệ phương trình:
\[
\begin{cases}
x - 3y + 4 = 0 \\
2x + 3y - 1 = 0
\end{cases} \Rightarrow \begin{cases}
x = -1 \\
y = 1
\end{cases}
\]
Kết quả ta có: \( A(-1; 1) \).
- Tính khoảng cách từ A đến Δ:
\[ d(A, Δ) = \frac{|3 \times (-1) + 1 + 16|}{\sqrt{3^2 + 1^2}} = \frac{| -3 + 1 + 16|}{\sqrt{9 + 1}} = \frac{14}{\sqrt{10}} \]
Ví dụ 3: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có \( A(3; - 4), B(1; 5), C(3; 1) \). Tính diện tích tam giác ABC.
Hướng dẫn giải:
- Đầu tiên, ta tính phương trình đường thẳng BC:
\[ 2(x-1) + 1(y-5) = 0 \Rightarrow 2x + y - 7 = 0 \]
- Tiếp theo, khoảng cách từ điểm A đến đường thẳng BC là:
\[ d(A, BC) = \frac{|2 \times 3 + (-4) - 7|}{\sqrt{2^2 + 1^2}} = \frac{|6 - 4 - 7|}{\sqrt{5}} = \frac{5}{\sqrt{5}} = \sqrt{5} \]
\[ BC = \sqrt{(3-1)^2 + (1-5)^2} = 2\sqrt{5} \]
- Cuối cùng, tính diện tích tam giác ABC:
\[ S = \frac{1}{2} \times d(A, BC) \times BC = \frac{1}{2} \times \sqrt{5} \times 2\sqrt{5} = 5 \]
3. Bài tập luyện tập tính khoảng cách từ một điểm đến một đường thẳng
Sau khi đã tìm hiểu lý thuyết và các ví dụ cụ thể, bạn có thể thử sức với một số bài tập dưới đây.
Câu 1:
Khoảng cách từ điểm \( M(1; -1) \) đến đường thẳng \( (a): 3x - 4y - 21 = 0 \) là:
A. 1
B. 2
C. 45
D. 145
Câu 2:
Khoảng cách từ điểm O đến đường thẳng \( d:\frac{x}{6}+\frac{y}{8}=1 \) là:
A. 4,8
B. 110
C. 1
D. 6
Câu 3:
Khoảng cách từ điểm \( M(2; 0) \) đến đường thẳng là:
A. 2
B. \( \frac{2}{5} \)
C. \( \frac{10}{\sqrt{5}} \)
D. \( \frac{\sqrt{5}}{2} \)
Các câu hỏi trên đây không chỉ giúp bạn thực hành mà còn củng cố thêm lý thuyết đã học. Hãy cố gắng làm thử để kiểm tra kiến thức của mình nhé!
---
Bài viết trên đây đã tổng hợp toàn bộ công thức lý thuyết và cách áp dụng giải quyết các bài toán về khoảng cách từ một điểm đến một đường thẳng. Hy vọng thông qua tài liệu này, các bạn học sinh sẽ có thêm nguồn tài liệu hữu ích để ôn tập và chuẩn bị cho kỳ thi sắp tới. Để tìm hiểu thêm nhiều kiến thức bổ ích khác, hãy thường xuyên truy cập vào trang web VUIHOC!