Hình tam giác là một trong những hình học cơ bản mà học sinh gặp đầu tiên trong môn Toán. Một trong những khía cạnh quan trọng của hình tam giác là tính chu vi, không chỉ trong học tập mà còn trong các ứng dụng thực tiễn. Trong bài viết này, chúng ta sẽ tìm hiểu sâu về tính chu vi hình tam giác với nhiều loại hình khác nhau như tam giác thường, tam giác vuông, tam giác đều và tam giác cân. Đồng thời, chúng ta sẽ cùng khám phá cách tính chu vi tam giác trong không gian.
1. Tính chu vi tam giác thường
1.1 Định nghĩa tam giác thường
Tam giác thường là hình tam giác có ba cạnh không bằng nhau, tức là mỗi cạnh có độ dài khác nhau.
1.2 Công thức tính chu vi
Công thức tính chu vi hình tam giác thường rất đơn giản:
P = a + b + c
Trong đó:
- P là chu vi tam giác.
- a, b, c là độ dài của ba cạnh của tam giác.
1.3 Ví dụ minh hoạ
Giả sử chúng ta có tam giác với chiều dài các cạnh lần lượt là 4 cm, 8 cm và 9 cm. Tính chu vi tam giác này.
Áp dụng công thức:
P = 4 + 8 + 9 = 21 cm
2. Công thức tính chu vi tam giác cân
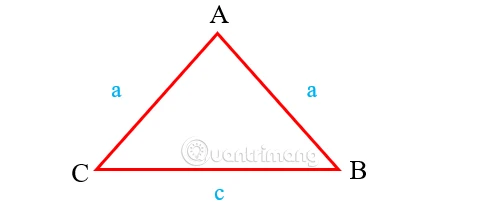
2.1 Định nghĩa tam giác cân
Tam giác cân là tam giác có hai cạnh và hai góc bằng nhau. Đỉnh của tam giác cân là giao điểm của hai cạnh bên.
2.2 Công thức tính chu vi
Công thức tính chu vi của tam giác cân:
P = 2a + c
Trong đó:
- a là độ dài của hai cạnh bên.
- c là độ dài của đáy tam giác.
2.3 Ví dụ minh hoạ
Cho tam giác cân với chiều dài hai cạnh bên là 7 cm và cạnh đáy là 5 cm.
Áp dụng công thức:
P = 2 * 7 + 5 = 19 cm
3. Cách tính chu vi tam giác đều
3.1 Định nghĩa tam giác đều
Tam giác đều là trường hợp đặc biệt của tam giác cân, nơi tất cả ba cạnh có độ dài bằng nhau.
3.2 Công thức tính chu vi
Công thức tính chu vi tam giác đều là:
P = 3 x a
Trong đó:
- P là chu vi tam giác đều.
- a là chiều dài của một cạnh.
3.3 Ví dụ minh hoạ
Nếu một tam giác đều có chiều dài cạnh là 5 cm, ta có thể tính chu vi như sau:
P = 3 x 5 = 15 cm
4. Chu vi tam giác vuông
4.1 Định nghĩa tam giác vuông
Tam giác vuông là hình tam giác có một góc vuông (góc 90 độ).
4.2 Công thức tính chu vi
Công thức tính chu vi tam giác vuông cũng giống như tam giác thường:
P = a + b + c
Trong đó:
- a và b là chiều dài hai cạnh góc vuông.
- c là cạnh huyền.
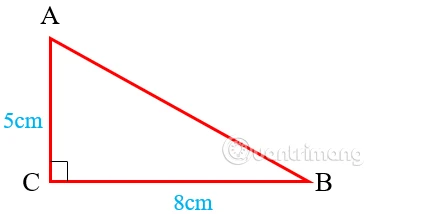
4.3 Ví dụ minh hoạ
Giả sử chúng ta có tam giác vuông có chiều dài các cạnh như sau: CA = 6 cm, CB = 7 cm và AB (cạnh huyền) = 10 cm.
Áp dụng công thức:
P = 6 + 7 + 10 = 23 cm
Ngoài ra, ta có thể tính chu vi khi biết hai cạnh góc vuông. Ví dụ:
Cho tam giác vuông với
CA = 5 cm và
CB = 8 cm. Để tìm cạnh huyền AB, ta sử dụng định lý Pythagore:
AB² = CA² + CB²
AB² = 5² + 8² = 25 + 64 = 89
AB = √89 ≈ 9.43 cm
Tính chu vi tam giác vuông CAB là:
P = 5 + 8 + 9.43 ≈ 22.43 cm
5. Tính chu vi tam giác trong không gian
5.1 Bài toán thí dụ
Giả sử trong không gian cho mặt phẳng Oxy, ta có hai điểm A(1;3), B(4;2). Cần tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB và tính chu vi tam giác OAB.
5.2 Giải quyết bài toán
Tìm tọa độ D:
Điểm D nằm trên trục tọa độ Ox nên tọa độ của D là (x;0).
Ta có khoảng cách:
DA = √((1-x)² + 3²)
DB = √((4-x)² + 2²)
DA = DB dẫn đến:
(1-x)² + 9 = (4-x)² + 4
Giải phương trình trên ta có:
x = 5/3 ⇒ D(5/3; 0)
Tính chu vi tam giác OAB:
Dùng công thức tính độ dài các đoạn đường:
- OA = √(1² + 3²) = √10
- OB = √(4² + 2²) = √20
- AB = √((4-1)² + (2-3)²) = √10
Do đó:
Chu vi tam giác OAB = OA + OB + AB = √10 + √20 + √10 = 2√10 + √20
6. Tổng kết
Việc tính chu vi hình tam giác là kiến thức toán học cơ bản nhưng rất cần thiết và ứng dụng trong nhiều lĩnh vực khác nhau. Qua bài viết này, bạn đã tìm hiểu về cách tính chu vi cho các loại tam giác khác nhau và cả trong không gian. Hy vọng với những kiến thức trên, bạn sẽ tự tin hơn khi giải quyết các bài toán liên quan đến hình tam giác trong học tập cũng như trong thực tiễn.
Nếu có bất kỳ câu hỏi nào hay muốn tham khảo thêm về các chủ đề liên quan đến hình học, đừng ngần ngại để lại câu hỏi nhé!