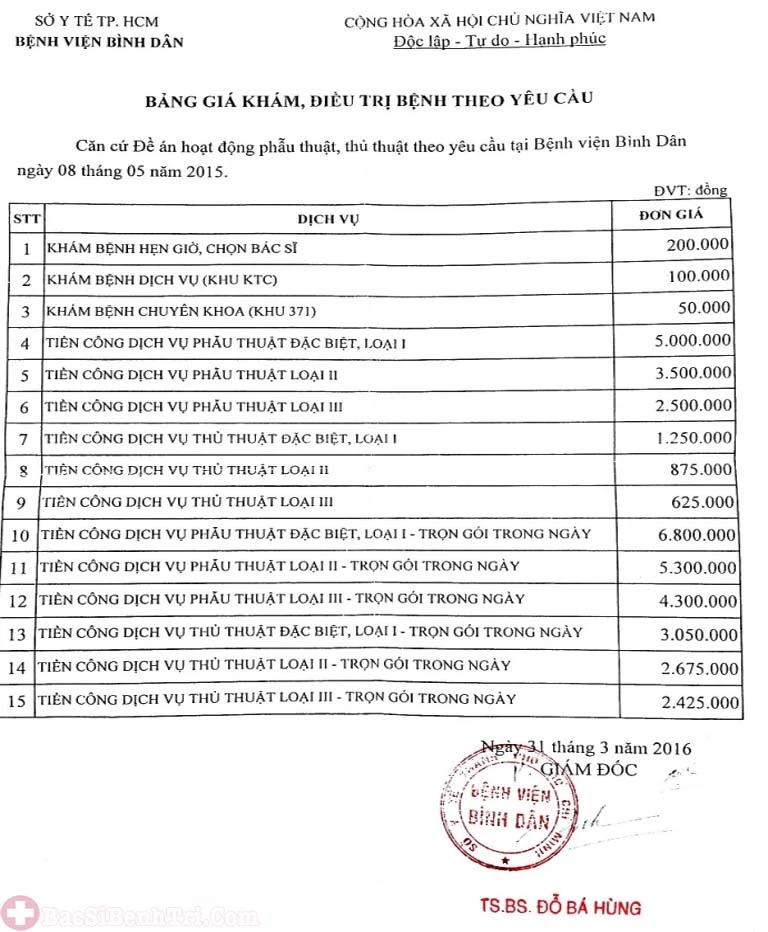
Khoảng cách từ một điểm đến mặt phẳng là một khái niệm quan trọng trong hình học không gian, được sử dụng rộng rãi trong toán học và các lĩnh vực liên quan như vật lý và kỹ thuật. Trong bài viết này, chúng ta sẽ cùng khám phá chi tiết về định nghĩa, công thức và các phương pháp tính khoảng cách từ điểm đến mặt phẳng, cũng như các bài tập thực hành để củng cố kiến thức.
Định Nghĩa Khoảng Cách Từ Điểm Đến Mặt Phẳng
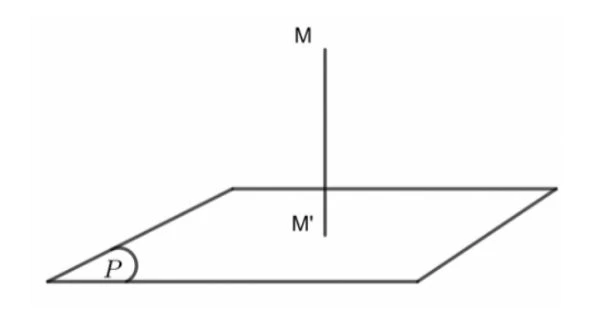
Cho một điểm \( M \) và một mặt phẳng \( P \) bất kỳ, khoảng cách từ điểm \( M \) đến mặt phẳng \( P \) được định nghĩa là khoảng cách giữa hai điểm \( M \) và \( H \), với \( H \) là hình chiếu của \( M \) lên mặt phẳng \( P \). Ký hiệu khoảng cách này là:
\[ d(M, (P)) = MH \]
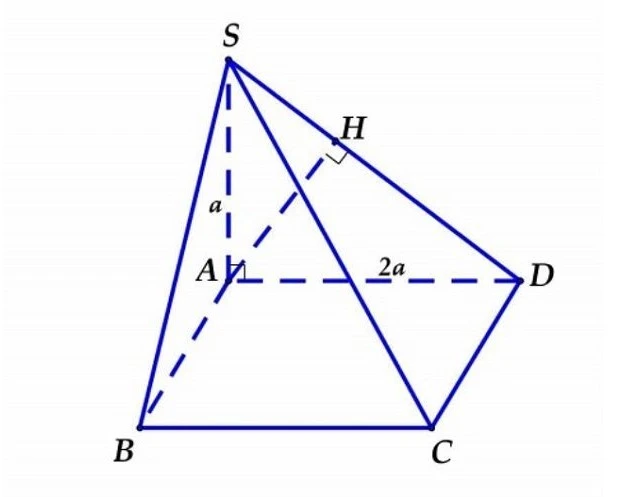
Hình ảnh dưới đây minh họa rõ hơn về khái niệm này:
Công Thức Tính Khoảng Cách Từ Điểm Đến Mặt Phẳng Trong Không Gian Tọa Độ
Trong không gian tọa độ \( Oxyz \), cho điểm \( M \) có tọa độ \( (\alpha, \beta, \gamma) \) và mặt phẳng \( P \) có phương trình dạng:
\[ ax + by + cz + d = 0 \]
Công thức tổng quát để tính khoảng cách từ điểm \( M \) đến mặt phẳng \( P \) được tính như sau:
\[ d(M, (P)) = \frac{|a\alpha + b\beta + c\gamma + d|}{\sqrt{a^2 + b^2 + c^2}} \]
Các Phương Pháp Tính Khoảng Cách Từ Điểm Đến Mặt Phẳng
Phương Pháp Số 1: Dựa Vào Định Nghĩa
Theo đúng như định nghĩa, để tính được khoảng cách từ điểm \( M \) tới mặt phẳng \( P \), chúng ta sẽ tìm hình chiếu của \( M \) trên mặt phẳng (được gọi là điểm \( H \)) và sau đó tính độ dài \( MH \) dựa trên công thức tính khoảng cách.
Phương Pháp Số 2: Tính Khoảng Cách Gián Tiếp
Chúng ta có thể tìm một điểm \( H' \) sao cho đường thẳng đi qua \( M \) và \( H' \) song song với mặt phẳng \( P \). Khi đó, ta có thể suy ra rằng khoảng cách từ \( M \) đến mặt phẳng \( P \) bằng khoảng cách từ \( H' \) đến \( P \):
\[ d(M, (P)) = d(H', (P)) \]
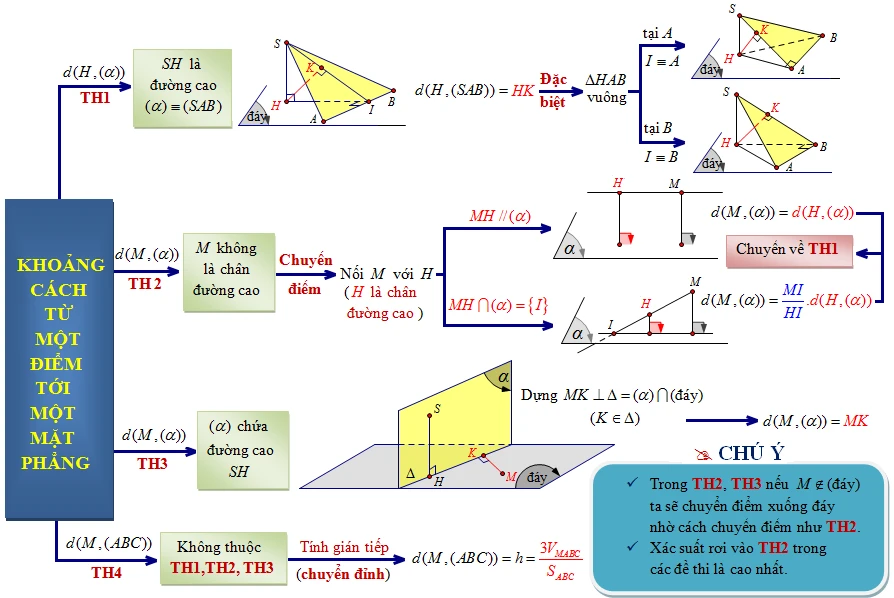
Phương Pháp Số 3: Sử Dụng Tam Giác Đồng Dạng
Chúng ta có thể tìm một điểm \( O \) xác định, sau đó tìm giao điểm của \( OA \) với mặt phẳng \( P \) là \( I \). Từ đó, chúng ta tính khoảng cách bằng cách sử dụng định lý Ta-lét:
\[ \frac{d(O, (alpha))}{d(A, (alpha))} = \frac{OI}{AI} \]
Ứng Dụng Các Phương Pháp Tính
Với ba phương pháp đã liệt kê, học sinh có thể dễ dàng tính được khoảng cách từ bất kỳ điểm nào đến một mặt phẳng cho trước. Về cơ bản, đối với các bài tập dạng này, học sinh cần đưa bài toán về dạng tìm khoảng cách từ điểm đó với hình chiếu của nó trên mặt phẳng hoặc sử dụng định lý Ta-lét và tam giác đồng dạng để tính khoảng cách.

Bài Tập Luyện Tập Tính Khoảng Cách Từ Một Điểm Đến Một Mặt Phẳng

Bài Tập 1
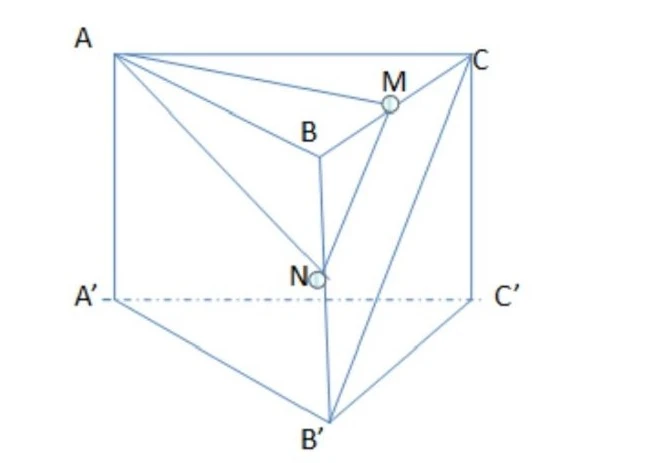
Cho lăng trụ đứng \( ABC.A'B'C' \) với đáy là một tam giác vuông cân \( ABC \) với \( BC = BA = a \), độ dài cạnh bên \( AA' = a\sqrt{2} \). Gọi trung điểm của đoạn thẳng \( BC \) là \( M \). Hãy tính khoảng cách giữa hai đường thẳng \( AM \) và \( B'C' \).
Hướng Dẫn Giải
Gọi trung điểm của cạnh bên \( BB' \) là \( N \). Đoạn thẳng \( MN \) là đường trung bình của tam giác \( BB'C \).
Suy ra: \( B'C \) song song \( MN \) \( \Rightarrow B'C \) song song với mặt phẳng \( (AMN) \).
Vậy ta có khoảng cách từ \( B'C \) đến mặt đến \( AM \) là:
\[ d(B'C; AM) = d(B'C; (AMN)) = d(B'; (AMN)) \]
Mà \( BB' \) giao với mặt phẳng \( (AMN) \) tại điểm \( N \), mà \( N \) là trung điểm của \( BB' \).
Suy ra:
\[ d(B'; (AMN)) = d(B; (AMN)) \]
Ta có: Hình chóp \( A.BMN \) có \( BA, BM, BN \) có một góc vuông.
Bài Tập 2
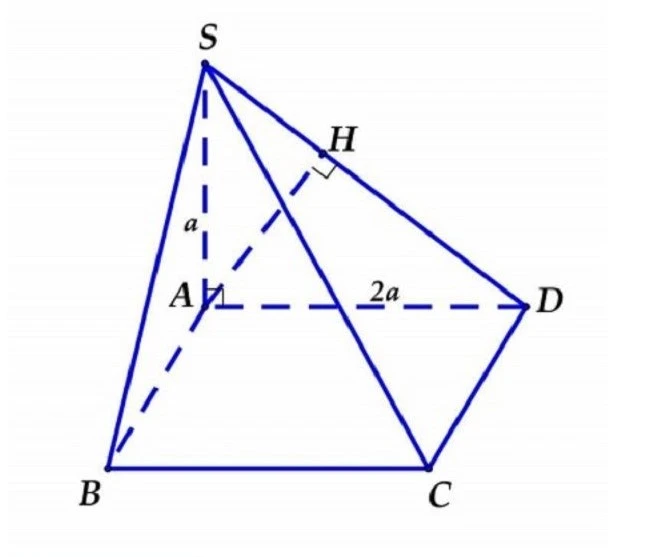
Cho hình chóp \( S.ABCD \) có đáy là hình chữ nhật \( ABCD \), biết độ dài cạnh \( AD = 2a \) và vuông góc với đáy, cạnh \( SA \) có độ dài là \( a \). Hãy tính khoảng cách từ điểm \( A \) tới mặt phẳng \( (SCD) \).
Hướng Dẫn Giải
Trong mặt phẳng \( (SAD) \), ta kẻ đường thẳng \( AH \) vuông góc với đoạn thẳng \( SD \) (với điểm \( H \) nằm trên đoạn thẳng \( SD \)).
Do \( CD \) vuông góc \( AD \) và \( CD \) vuông góc \( SA \).
Suy ra: \( SA \) vuông góc với mặt phẳng \( (SAD) \).
Bài Tập 3
Cho hình chóp \( S.ABC \) có đáy là tam giác vuông \( ABC \) tại \( B \). Biết rằng độ dài các cạnh \( BA = a \), \( BC = 2a \) và cạnh \( SA = 2a \), đồng thời cạnh \( SA \) vuông góc với mặt phẳng \( (ABC) \). Gọi điểm \( K \) là hình chiếu của \( A \) lên đường thẳng \( SC \). Tính khoảng cách từ điểm \( K \) đến mặt phẳng \( (SAB) \).
Hướng Dẫn Giải
Từ điều kiện đề bài, ta có \( SA \) vuông góc với mặt phẳng \( (ABC) \) \( \Rightarrow SA \perp BC \).
Từ đó, ta có thể suy ra rằng khoảng cách từ \( K \) đến mặt phẳng \( (SAB) \) là:
\[ d(K; (SAB)) = KH \]
Bài Tập 4
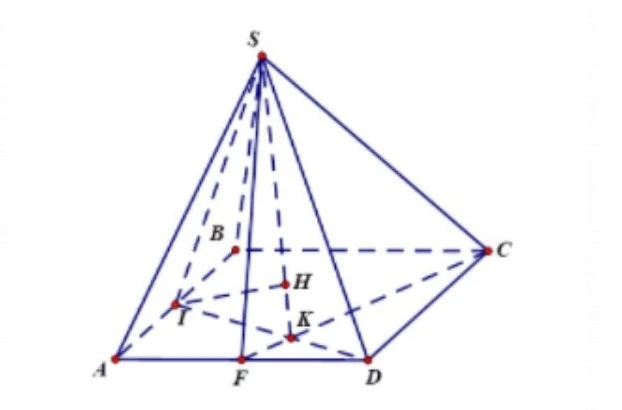
Cho một hình chóp \( S.ABCD \), có đáy là hình vuông \( ABCD \) có cạnh là \( a \). Biết rằng tam giác \( SAB \) là một tam giác đều và mặt phẳng \( (SAB) \) vuông góc với mặt phẳng \( (ABCD) \). Gọi 2 điểm \( I \) và \( F \) lần lượt là trung điểm của \( AB \) và \( AD \), hãy tính khoảng cách từ điểm \( I \) tới mặt phẳng \( SFC \).
Hướng Dẫn Giải
Gọi điểm \( K \) là điểm giao nhau của 2 đoạn thẳng \( ID \) và \( FC \).
Kẻ đoạn thẳng \( IH \) vuông góc với \( SK \) (với điểm \( H \) nằm trên đoạn thẳng \( SK \)).
Ta có:
\[ SI \perp (ABCD) \quad \Rightarrow SI \perp FC \]
Do đó, khoảng cách từ \( I \) đến mặt phẳng \( SFC \) là:
\[ d(I, (SFC)) = IH \]
Bài Tập 5
Cho một hình chóp \( S.ABCD \) có đáy là một hình thang vuông \( ABCD \) vuông tại \( A \) và \( D \), biết rằng độ dài cạnh \( AD = AB = a \) và độ dài cạnh \( CD = 2a \), \( SD = a \) với \( SD \) vuông góc với mặt phẳng \( (ABCD) \).
Hướng Dẫn Giải
Gọi trung điểm của cạnh \( CD \) là điểm \( M \).
Gọi giao diện của 2 đường thẳng \( BC \) và \( AD \) là điểm \( E \).
- a. Kẻ đoạn thẳng \( DH \) vuông góc với \( SB \) thuộc mặt phẳng \( (SBD) \) với điểm \( H \) nằm trên cạnh \( SB \).
- b. Tính khoảng cách từ điểm \( A \) tới mặt phẳng \( (SBC) \).
Kết Luận
Trên đây là toàn bộ kiến thức cũng như các phương pháp tính khoảng cách từ điểm đến mặt phẳng trong chương trình toán 11. Để tìm hiểu thêm về kiến thức của các môn học khác, các em học sinh có thể truy cập vào các trang học trực tuyến như VUIHOC. Chúc các em đạt kết quả tốt trong các kỳ thi trong tương lai.
Bài Viết Tham Khảo Thêm
Hy vọng bài viết này mang đến cho bạn một cái nhìn rõ ràng và sâu sắc về khoảng cách từ điểm đến mặt phẳng, cũng như các kỹ thuật tính toán hữu ích trong giải bài tập.