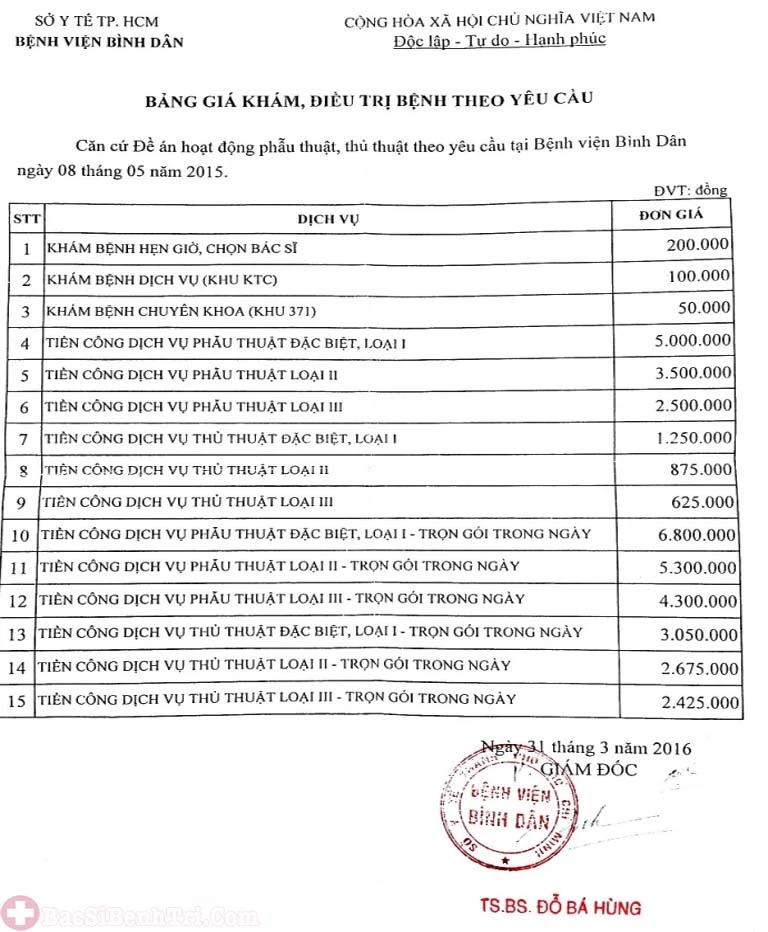
Diện tích tam giác là một trong những kiến thức cơ bản mà học sinh cần nắm vững trong môn Toán học. Trong số các loại tam giác, tam giác vuông có đặc điểm và công thức tính diện tích riêng biệt, rất hữu ích trong việc giải quyết bài tập. Hãy cùng
The Dewey Schools khám phá cách tính diện tích tam giác vuông một cách chi tiết và dễ hiểu nhất nhé!
Hình Tam Giác Vuông Là Gì?
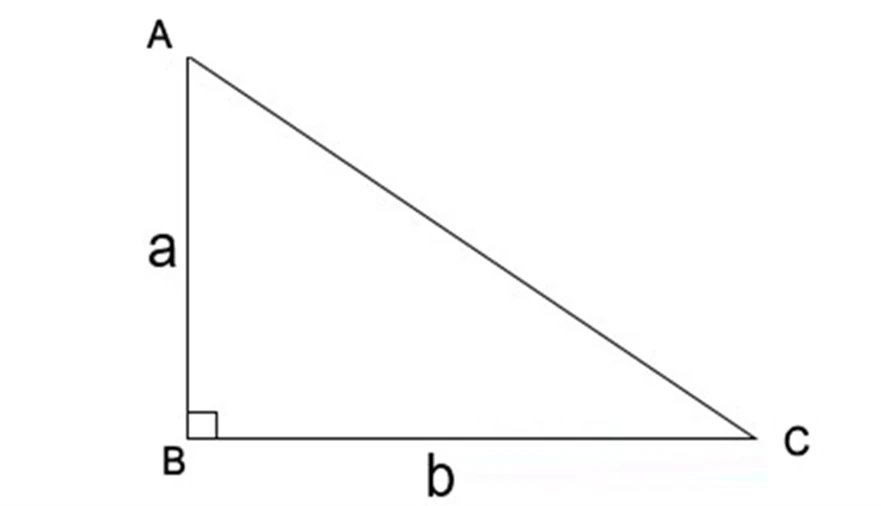
Định Nghĩa
Tam giác vuông là một loại tam giác có một góc bằng 90 độ, tức là một góc vuông. Hai cạnh tạo thành góc vuông được gọi là
cạnh góc vuông, trong khi cạnh đối diện với góc vuông được gọi là
cạnh huyền.

Tính Chất Của Tam Giác Vuông
- Tổng Các Góc: Tổng của ba góc trong tam giác vuông luôn bằng 180 độ, trong đó một góc là 90 độ.
- Định Lý Pythagoras: Đối với tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông. Cụ thể, nếu a và b là độ dài của hai cạnh góc vuông, c là độ dài của cạnh huyền, ta có:
\[
c^2 = a^2 + b^2
\]

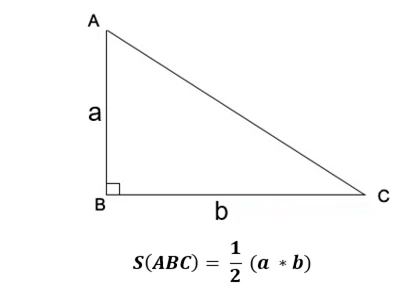
Công Thức Tính Diện Tích Tam Giác Vuông
Để tính diện tích tam giác vuông, chúng ta sử dụng công thức đơn giản. Diện tích tam giác vuông được tính như sau:
\[
S = \frac{1}{2} \times a \times b
\]
Trong đó:
- \( S \) là diện tích tam giác.
- \( a \) và \( b \) là độ dài của hai cạnh góc vuông.
Ví dụ Cụ Thể
Giả sử ta có một tam giác vuông ABC với:
- Cạnh góc vuông AB = 6 cm
- Cạnh góc vuông AC = 8 cm
Diện tích tam giác ABC sẽ được tính như sau:
\[
S = \frac{1}{2} \times 6 \times 8 = 24 \, \text{cm}^2
\]
Các Phương Pháp Khác Để Tính Diện Tích Tam Giác Vuông
Ngoài công thức cơ bản trên, còn có một số phương pháp khác giúp bạn tính diện tích tam giác vuông dựa trên thông tin khác mà bạn đã biết.
1. Tính Diện Tích Khi Biết Cạnh Huyền và Một Cạnh Góc Vuông
Nếu bạn biết độ dài của cạnh huyền và một cạnh góc vuông, bạn có thể tìm ra diện tích bằng cách trước tiên tìm độ dài cạnh còn lại dựa vào định lý Pythagoras. Ví dụ:
Giả sử tam giác vuông ABC có cạnh huyền BC = 10 cm và cạnh góc vuông AB = 6 cm, ta tìm cạnh còn lại AC:
\[
AC^2 = BC^2 - AB^2 = 10^2 - 6^2 = 100 - 36 = 64 \Rightarrow AC = 8 \, \text{cm}
\]
Diện tích sẽ là:
\[
S = \frac{1}{2} \times AB \times AC = \frac{1}{2} \times 6 \times 8 = 24 \, \text{cm}^2
\]
2. Tính Diện Tích Khi Biết Diện Tích và Một Cạnh
Nếu bạn biết diện tích của tam giác vuông và độ dài một cạnh, bạn có thể tìm ra chiều dài của cạnh còn lại. Ví dụ:
Giả sử diện tích S = 30 cm² và cạnh góc vuông AB = 5 cm, ta có:
\[
30 = \frac{1}{2} \times 5 \times b \Rightarrow b = \frac{30 \times 2}{5} = 12 \, \text{cm}
\]
Dạng Bài Tập Thường Gặp Về Tính Diện Tích Tam Giác Vuông
Bài Tập 1: Tính Diện Tích Khi Biết Chiều Dài Hai Cạnh
Cho tam giác vuông ABC với cạnh góc vuông AB = 3 cm và AC = 4 cm. Tính diện tích S.
Lời Giải:
\[
S = \frac{1}{2} \times AB \times AC = \frac{1}{2} \times 3 \times 4 = 6 \, \text{cm}^2
\]
Bài Tập 2: Tính Diện Tích Khi Biết Cạnh Huyền và Cạnh Góc Vuông
Cho tam giác vuông ABC với cạnh huyền BC = 13 cm và cạnh góc vuông AB = 5 cm. Tính diện tích S.
Lời Giải:
Tìm cạnh AC:
\[
AC^2 = BC^2 - AB^2 = 13^2 - 5^2 = 169 - 25 = 144 \Rightarrow AC = 12 \, \text{cm}
\]
Tính diện tích:
\[
S = \frac{1}{2} \times AB \times AC = \frac{1}{2} \times 5 \times 12 = 30 \, \text{cm}^2
\]
Các Câu Hỏi Thường Gặp Về Cách Tính Diện Tích Tam Giác Vuông
1. Làm Thế Nào Để Tính Diện Tích Tam Giác Vuông Khi Chỉ Biết Một Cạnh?
Để tính diện tích tam giác vuông khi chỉ biết một cạnh, bạn cần thêm thông tin về chiều cao tương ứng hoặc cạnh còn lại để áp dụng công thức tính diện tích.
2. Có Thể Tính Diện Tích Tam Giác Vuông Trong Không Gian 3 Chiều Không?
Có, diện tích tam giác vuông trong không gian 3 chiều cũng được tính bằng cách sử dụng các tọa độ. Công thức sẽ dựa vào các vectơ được sinh ra từ các điểm trong không gian.
Kết Luận
Việc nắm vững cách tính diện tích tam giác vuông không chỉ giúp bạn giải quyết bài tập một cách hiệu quả mà còn là nền tảng cho nhiều kiến thức toán học sau này. Hãy thường xuyên luyện tập và áp dụng các công thức mà
The Dewey Schools đã cung cấp để trở thành bậc thầy về diện tích tam giác vuông nhé! Chúc bạn học tốt!