21/11/2024 18:46

Công Thức Tính Thể Tích Khối Trụ Tròn Xoay Và Bài Tập

1. Khối trụ tròn xoay là gì?

Khối trụ tròn xoay là một trong những khái niệm cơ bản trong hình học không gian. Trong không gian 3 chiều, khi một hình phẳng (thường là hình chữ nhật) quay quanh một trục cố định, chúng ta sẽ tạo ra một khối hình ba chiều, gọi là khối trụ tròn xoay. Cụ thể, hình trụ tròn xoay được hình thành khi đường trung bình của hình chữ nhật quay quanh một trục cố định, và diện tích mặt đáy là một hình tròn.

Khối trụ tròn xoay

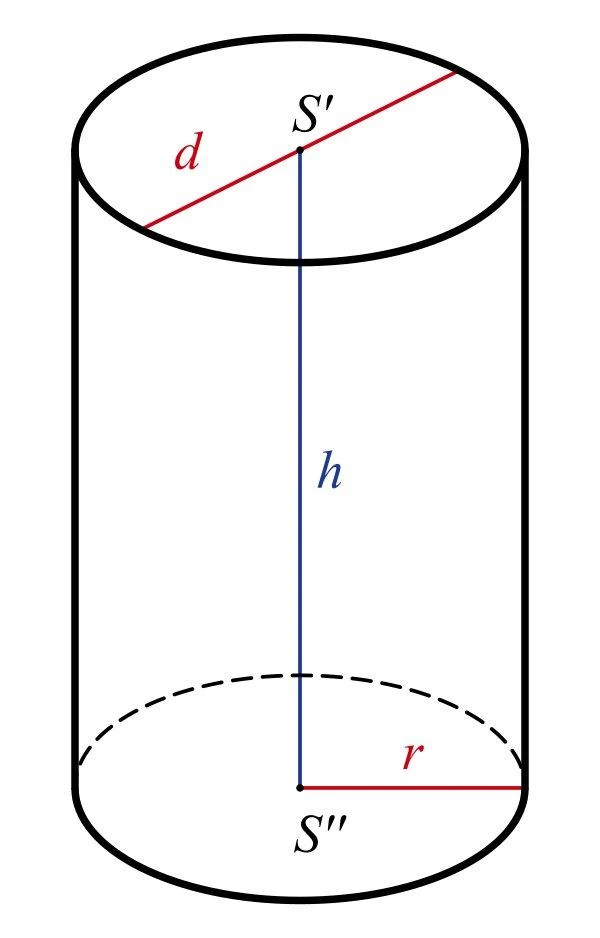
Khối trụ không chỉ bao gồm bề mặt bên ngoài mà còn chứa cả không gian bên trong. Thể tích của khối trụ tròn xoay sẽ được xác định bởi kích thước của mặt đáy (hình tròn) và chiều cao của nó.

2. Công thức tính thể tích hình trụ tròn xoay

Để tính thể tích của khối trụ tròn xoay, chúng ta áp dụng công thức sau:

$V = \pi.r^{2}.h$

Trong đó:

V là thể tích của khối trụ.
r là bán kính của mặt đáy khối trụ.
h là chiều cao của khối trụ, tức là khoảng cách giữa hai đáy.
π là hằng số pi (khoảng 3.14).

Đơn vị của thể tích thường là m³. Các bạn có thể thấy rằng công thức tính thể tích khối trụ tròn xoay tương tự như công thức tính thể tích của khối lăng trụ, khi cả hai đều dựa trên diện tích đáy nhân với chiều cao.

3. Các dạng bài tập về thể tích của khối trụ tròn xoay

Khi làm bài tập về thể tích khối trụ tròn xoay, chúng ta sẽ gặp các dạng bài cơ bản với ba đại lượng chính: thể tích (V), bán kính đáy (r) và chiều cao (h). Dưới đây là ba dạng bài tập phổ biến mà bạn có thể sẽ gặp:

3.1. Dạng 1: Tìm bán kính đáy của khối trụ tròn xoay

Để tìm bán kính đáy của khối trụ, bạn có thể áp dụng các cách sau:

Nếu đề bài cho đường kính của mặt đáy, bạn chỉ cần chia đôi đường kính để tìm bán kính.
Nếu đề bài cho chu vi mặt đáy, bạn lấy chu vi chia cho $2\pi$ để tìm bán kính.

Ví dụ: Cho khối trụ tròn xoay có thể tích bằng $\pi a^{3}$ , chiều cao là h = 2a. Tìm bán kính đáy r của khối trụ đó?

Lời giải:

Áp dụng công thức tính thể tích: $V = r^{2}.h$

Suy ra: $r = \sqrt{\frac{V}{\pi h}}$

3.2. Dạng 2: Tìm diện tích đáy tròn

Để tính diện tích đáy tròn của khối trụ, chúng ta sử dụng công thức tính diện tích hình tròn: $(\pi.r^{2})$ .

Ví dụ: Cho khối trụ tròn xoay có diện tích toàn phần gấp 2 lần diện tích xung quanh và có bán kính đáy bằng 6cm. Tính thể tích khối trụ đó.

Giải:

Vì diện tích toàn phần của khối trụ gấp 2 lần diện tích xung quanh của nó nên:

$2.2.\pi.r.h = 2.\pi.r.h.(r + h)$

$\Rightarrow 2.h = 6 + h \Rightarrow h = 6 (cm)$

$\Rightarrow V = \pi.r^{2}.h = \pi.6^{2}.6 = \sim 678,6 cm^{3}$

Vậy thể tích của khối trụ tròn xoay là 678,6 cm³.

3.3. Dạng 3: Tìm chiều cao của hình trụ

Trong một số bài tập, độ dài đường chéo của mặt đáy có thể được cho, và bạn có thể sử dụng định lý Pytago để tính chiều cao của khối trụ.

Ví dụ: Cho khối trụ có thể tích bằng $12\pi$, chu vi đáy là $2\pi$. Tính thể tích của khối trụ đó.

Lời giải:

Bán kính đáy của khối trụ tròn xoay là:

$r = \frac{2\pi}{2\pi} = 1$

Chiều cao của khối trụ là:

$h = \frac{V}{\pi r^{2}} = \frac{12\pi}{\pi 1^{2}} = 12$

Vậy chiều cao của khối trụ là 12.

4. Một số bài tập tính thể tích khối trụ tròn xoay (kèm lời giải chi tiết)

Bài 1: Cho hình trụ tròn xoay có hai đáy là hai đường tròn có tâm O và O', A và B lần lượt nằm trên hai đường tròn đó. Biết rằng AB tạo với trục OO' góc α và AB = a. Tính thể tích khối trụ theo α và a, biết khoảng cách giữa AB và OO' bằng d.

Lời giải:

Gọi điểm C là đường chiếu của điểm A lên đường tròn tâm O'. I là trung điểm của BC. Góc giữa AB và OO' là góc BAC. Vậy chiều cao của khối trụ là h = OO' = AB cosα = a.cosα.

Ta có chiều dài đoạn IC là: $IC = \frac{1}{2} BC = \frac{1}{2}a.sin\alpha$

Vậy bán kính đáy khối trụ là: $r = \sqrt{IC^{2} + O'I^{2}} = \sqrt{\frac{1}{4}a^{2}sin^{2}\alpha + d^{2}}$

Thể tích của khối trụ đã cho là: $V = \pi r^{2}h = \pi (\frac{1}{4}a^{2}sin^{2}\alpha + d^{2})$

Bài 2: Cho khối trụ tròn xoay có đáy là hình tròn ngoại tiếp của tam giác đều cạnh a. Biết chiều cao khối trụ là 3a. Tính thể tích khối trụ tròn xoay đó.

Lời giải:

Bán kính đáy của khối trụ là: $r = \frac{a\sqrt{3}}{3}$

Thể tích của khối trụ đó là $V = \pi.r^{2}.h = \pi.(\frac{a^{3}}{3})^{2}.3a = \pi.a^{3}$

Vậy thể tích của khối trụ tròn xoay là $V = \pi.a^{3}$

Bài 3: Cho khối trụ có chu vi đáy bằng 20cm, diện tích xung quanh khối trụ bằng 14cm². Tính thể tích và chiều cao của khối trụ?

Lời giải:

Vì chu vi đáy bằng 20cm, diện tích xung quanh khối trụ bằng 14cm² nên:

$S_{xq} = 2\pi rh = 20h = 14 \Rightarrow h = \frac{14}{20} = 0,7 (cm)$

$2\pi r = 20 \Rightarrow r \sim 3,18 (cm)$

Thể tích của khối trụ đó là $V = 2\pi r^{2}h$

Vậy thể tích của khối trụ tròn xoay là V = 219,91cm³.

Ngoài ra, bạn cũng có thể tham khảo thêm những cách giải nhanh và thú vị hơn trong video bài giảng của thầy Tài về thể tích khối tròn xoay, cùng VUIHOC học nhé!

Trên đây là toàn bộ lý thuyết về khối trụ tròn xoay. Hy vọng sau bài viết này, bạn đã nắm được định nghĩa, công thức tính thể tích khối trụ tròn xoay và biết cách giải các bài tập liên quan đến hình trụ. Đừng quên truy cập Vuihoc.vn và đăng ký tài khoản để học thêm nhiều công thức toán hình 12 bổ ích khác nhé!

Tham khảo thêm:

Bộ Sách Thần Tốc Luyện Đề Toán - Lý - Hóa THPT Có Giải Chi Tiết

>>> Xem thêm:

12 Công thức tính thể tích khối chóp kèm ví dụ cụ thể
Công thức tính thể tích khối lăng trụ tam giác đều
Công thức tính thể tích khối cầu nhanh và chính xác nhất
Công thức tính thể tích khối tròn xoay và bài tập vận dụng
Công thức tính thể tích khối trụ tròn xoay và bài tập
Công thức tính thể tích khối nón và bài tập

Link nội dung: https://citc-hou.edu.vn/cong-thuc-tinh-the-tich-khoi-tru-tron-xoay-va-bai-tap-a13163.html