I. Giới thiệu về hình lăng trụ và hình hộp
Trong toán học, hình học không gian là một lĩnh vực thú vị giúp chúng ta hiểu rõ hơn về các hình dạng và cấu trúc trong không gian ba chiều. Một trong những hình dạng cơ bản nhưng quan trọng mà chúng ta thường gặp là hình lăng trụ và hình hộp. Bài viết này sẽ giúp bạn khám phá sâu hơn về chúng, đặc biệt là hình hộp.
II. Hình Lăng Trụ
1. Định Nghĩa Hình Lăng Trụ
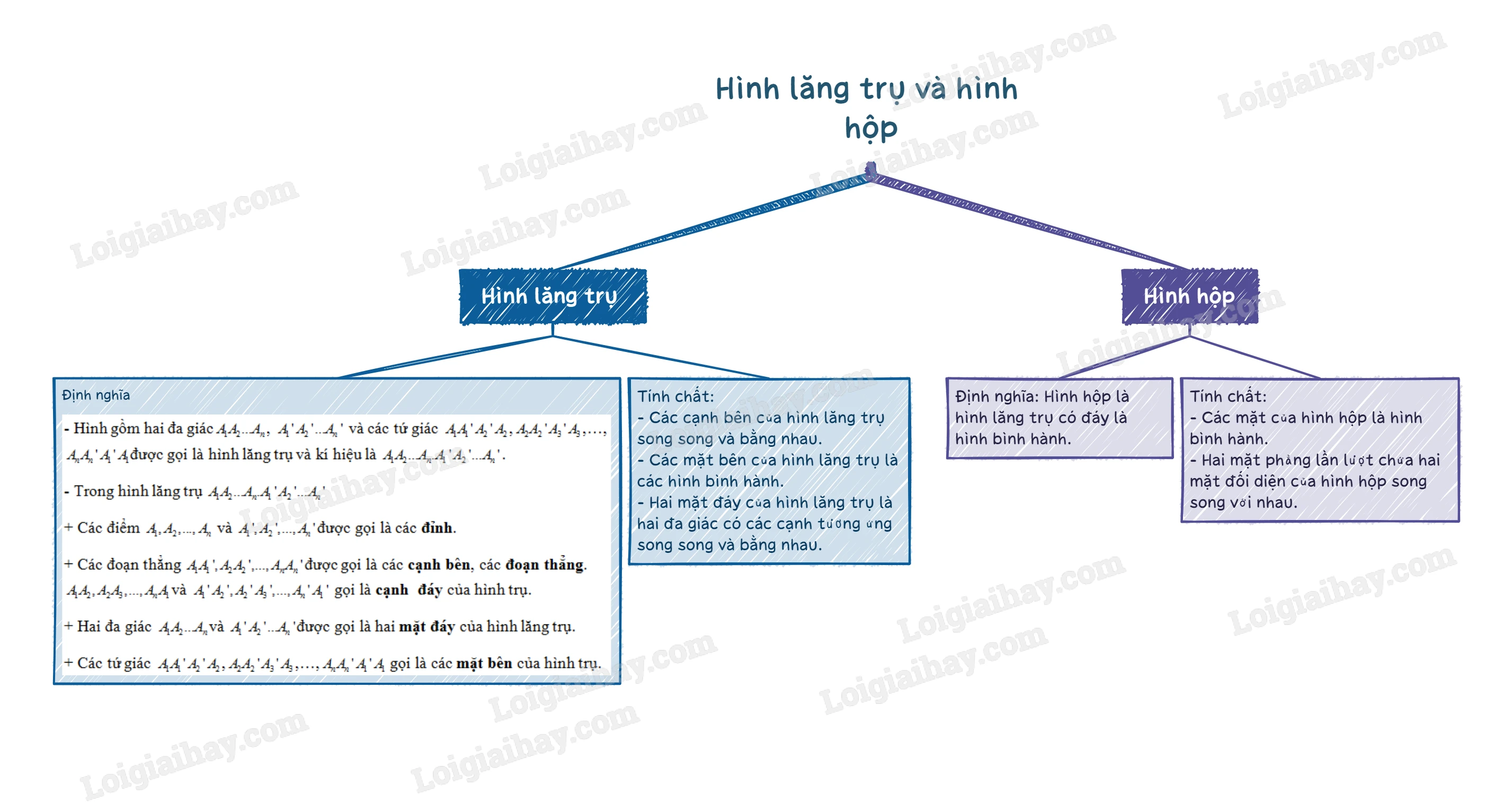
Hình lăng trụ là một loại hình khối được tạo thành từ hai đa giác song song và các tứ giác kết nối chúng. Cụ thể, hình lăng trụ được định nghĩa như sau:
- Các đỉnh: Gồm hai đa giác \({A_1}{A_2}...{A_n}\) và \({A_1}'{A_2}'...{A_n}'\).
- Cạnh bên: Các đoạn thẳng \({A_1}{A_1}', {A_2}{A_2}', \ldots, {A_n}{A_n}'\) là các cạnh bên.
- Cạnh đáy: Được xác định bởi các đoạn thẳng \({A_1}{A_2}, {A_2}{A_3}, \ldots, {A_n}{A_1}\) và \({A_1}'{A_2}', {A_2}'{A_3}', \ldots, {A_n}'{A_1}'\).
- Mặt đáy: Hai đa giác \({A_1}{A_2}...{A_n}\) và \({A_1}'{A_2}'...{A_n}'\) được gọi là hai mặt đáy của hình lăng trụ.
- Mặt bên: Các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\), \({A_2}{A_2}'{A_3}'{A_3}\), …, \({A_n}{A_n}'{A_1}'{A_1}\) là các mặt bên.
Chú ý rằng nếu đáy của lăng trụ là một tam giác, tứ giác, ngũ giác, … thì các loại lăng trụ tương ứng sẽ được gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác.
2. Tính Chất của Hình Lăng Trụ
- Các cạnh bên: Tất cả các cạnh bên của hình lăng trụ là song song và có độ dài bằng nhau.
- Mặt bên: Các mặt bên của hình lăng trụ là các hình bình hành.
- Mặt đáy: Hai mặt đáy của hình lăng trụ là các đa giác có các cạnh tương ứng song song và bằng nhau.
III. Hình Hộp
1. Định Nghĩa Hình Hộp
Hình hộp là một loại hình lăng trụ đặc biệt, trong đó đáy của nó là một hình bình hành. Hình hộp có những đặc điểm riêng biệt như sau:
- Mặt đối diện: Hai mặt không có đỉnh chung được gọi là hai mặt đối diện.
- Cạnh đối diện: Hai cạnh song song không nằm trong cùng một mặt phẳng gọi là hai cạnh đối diện.
- Đỉnh đối diện: Hai đỉnh không thuộc cùng một mặt gọi là hai đỉnh đối diện.
- Đường chéo: Đoạn thẳng nối hai đỉnh đối diện được gọi là đường chéo.
2. Tính Chất của Hình Hộp
- Mặt: Tất cả các mặt của hình hộp đều là hình bình hành.
- Mặt phẳng song song: Hai mặt phẳng chứa hai mặt đối diện của hình hộp là song song với nhau.
IV. Phân Loại Hình Hộp
1. Hình Hộp Chữ Nhật
Hình hộp chữ nhật là loại hình hộp mà các mặt đáy là hình chữ nhật. Các tính chất nổi bật của hình hộp chữ nhật bao gồm:
- Tất cả các góc đều vuông.
- Độ dài các cạnh khác nhau có thể khác nhau, nhưng chiều cao là cố định.
2. Hình Hộp Vuông
Hình hộp vuông là trường hợp đặc biệt của hình hộp chữ nhật, trong đó tất cả các cạnh đều bằng nhau. Các tính chất của hình hộp vuông bao gồm:
- Các mặt đều là hình vuông.
- Hình hộp vuông có độ đối xứng cao và thường được ứng dụng trong kiến trúc và thiết kế nội thất.
3. Hình Hộp Lập Phương
Hình hộp lập phương là hình hộp đặc biệt nhất, trong đó tất cả các cạnh đều bằng nhau và các mặt đều là hình vuông. Đặc điểm nổi bật của hình hộp lập phương:
- Tính đối xứng hoàn hảo.
- Dễ dàng trong việc tính toán thể tích và diện tích bề mặt.
V. Công Thức và Cách Tính
1. Thể Tích của Hình Hộp
Thể tích của hình hộp được tính bằng công thức:
\[ V = D \times R \times C \]
Trong đó:
- \( D \): diện tích đáy
- \( R \): chiều cao
- \( C \): chiều dài hoặc chiều rộng tùy thuộc vào loại hình hộp.
2. Diện Tích Bề Mặt
Diện tích bề mặt của một hình hộp được tính bằng công thức:
\[ S = 2(D \times R + D \times C + R \times C) \]
Trong đó, các ký hiệu giống như trên.
VI. Ứng Dụng của Hình Hộp trong Thực Tiễn
Hình hộp là một trong những hình khối phổ biến nhất trong cuộc sống hàng ngày và có nhiều ứng dụng trong các lĩnh vực khác nhau:
- Kiến trúc: Hình hộp được sử dụng để xây dựng các tòa nhà, văn phòng, và nhà ở.
- Đóng gói: Hình hộp là hình dạng lý tưởng để chứa đựng các sản phẩm như thùng carton, hộp quà, và nhiều loại bao bì khác.
- Thiết kế nội thất: Hình hộp thường thấy trong việc thiết kế các đồ nội thất như bàn, ghế, tủ kệ.
VII. Kết Luận
Hình hộp và hình lăng trụ không chỉ là những khái niệm cơ bản trong hình học mà còn có ứng dụng rộng rãi trong cuộc sống hàng ngày. Hiểu rõ về cấu trúc, tính chất và các loại hình hộp sẽ giúp chúng ta có cái nhìn sâu sắc hơn về không gian xung quanh. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và bổ ích về hình hộp, giúp bạn áp dụng vào học tập và cuộc sống. Nếu bạn còn thắc mắc hoặc muốn tìm hiểu sâu hơn về các loại hình khối khác, hãy theo dõi các bài viết tiếp theo của chúng tôi!