Tìm Hiểu Về Hình Lục Giác Đều Trong Hình Học

Hình lục giác đều là một trong những hình dạng đẹp và có tính ứng dụng cao trong cuộc sống và khoa học. Những đặc điểm riêng biệt của hình này đã làm cho nó trở thành một chủ đề thú vị trong toán học và các lĩnh vực khác. Dưới đây là một cái nhìn chi tiết hơn về hình lục giác đều, từ đặc điểm, công thức toán học đến ứng dụng thực tế, giúp bạn hiểu sâu hơn về nó.

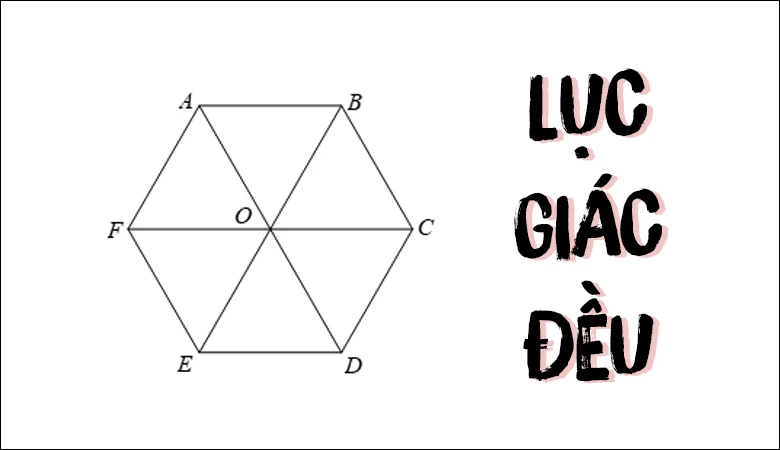
Đặc Điểm Của Hình Lục Giác Đều

1. Định Nghĩa Lục Giác Đều

Hình lục giác đều là một loại đa giác có sáu cạnh có độ dài bằng nhau và sáu góc bằng nhau. Điều này có nghĩa là mọi cạnh của lục giác đều (hay còn gọi là lục giác đều) đều có cùng độ dài, và mọi góc nội đều có giá trị bằng nhau.

2. Các Đặc Điểm Cơ Bản

• Độ dài cạnh: Mỗi cạnh của lục giác đều có độ dài bằng nhau.
• Góc nội: Mỗi góc trong của lục giác đều là \(120^\circ\).
• Tổng số đo các góc trong: Tổng số đo các góc trong của lục giác đều là \(720^\circ\).
• Tâm đối xứng: Tâm của đường tròn ngoại tiếp lục giác đều cũng chính là tâm đối xứng quay của hình.

3. Các Đặc Điểm Đối Xứng

Hình lục giác đều có tính đối xứng nổi bật:

• Có 6 trục đối xứng (tại các đỉnh và giữa các cạnh).
• Có tính đối xứng quay 60 độ, tức là bạn có thể quay hình lục giác đều quanh tâm và nó sẽ nhìn giống hệt như ban đầu sau mỗi 60 độ.

Công Thức Tính Toán Liên Quan Đến Lục Giác Đều

1. Tổng Góc Trong

Công thức tính tổng góc trong của một đa giác là: \[ \text{Tổng góc trong} = (n-2) \times 180^\circ \] Với \(n\) là số cạnh. Khi áp dụng cho lục giác đều (\(n = 6\)), ta có: \[ \text{Tổng góc trong} = (6-2) \times 180^\circ = 720^\circ \]

2. Góc Nội

Công thức tính góc nội của lục giác đều là: \[ \text{Góc nội} = \frac{(n-2) \times 180^\circ}{n} = \frac{(6-2) \times 180^\circ}{6} = 120^\circ \]

3. Bảng Tóm Tắt Các Đại Lượng

| Thông Số | Giá Trị | |------------------|---------------------| | Tổng số góc trong| 720 độ | | Góc mỗi đỉnh | 120 độ | | Tính đối xứng | 6 trục đối xứng | | Tâm đường tròn ngoại tiếp | Tâm đối xứng quay |

Các Ứng Dụng Thực Tế Của Lục Giác Đều

Lục giác đều không chỉ là một khái niệm toán học mà còn có nhiều ứng dụng thực tiễn. Dưới đây là một số lĩnh vực nổi bật mà lục giác đều được áp dụng.

1. Kiến Trúc Và Xây Dựng

• Gạch Lát Ốp Tường: Lục giác đều thường được sử dụng trong thiết kế gạch lát để tạo ra những hình khối bắt mắt và không gian hài hòa.
• Cấu Trúc Mái: Lục giác cũng xuất hiện trong thiết kế mái của các ngôi nhà, đặc biệt là trong các công trình kiến trúc châu Á.

2. Công Nghệ

• Mô Hình Hóa Phân Tử: Trong lĩnh vực vật liệu học, hình lục giác đều góp mặt trong mô hình hóa cấu trúc của các vật liệu như kim cương, graphene, và graphit, giúp nghiên cứu tính chất của chúng.
• Mạch Điện Tử: Trong thiết kế mạch điện tử, một số cấu trúc cũng áp dụng hình lục giác để tối ưu hóa không gian và tăng tính hiệu quả.

3. Nghệ Thuật Và Thiết Kế

• Thiết Kế Hoa Văn: Hình lục giác đều là hình dạng cơ bản trong nhiều mẫu hoa văn nghệ thuật, từ trang trí đồ nội thất đến sản phẩm thủ công.
• Sản Xuất Đồ Dùng: Lục giác cũng được áp dụng trong thiết kế các sản phẩm như khay đựng, đèn thả, mang lại tính thẩm mỹ cao và dễ sử dụng.

Phương Pháp Vẽ Lục Giác Đều

Có nhiều cách để vẽ hình lục giác đều, nhưng dưới đây là một số phương pháp đơn giản và hiệu quả nhất.

1. Sử dụng Compa và Thước Kẻ

• Bước 1: Vẽ một đường tròn với tâm O.
• Bước 2: Chọn một điểm A trên đường tròn làm điểm bắt đầu.
• Bước 3: Sử dụng compa, giữ nguyên độ dài bằng bán kính đường tròn, đặt đầu nhọn tại điểm A để đánh dấu một điểm B trên đường tròn.
• Bước 4: Tiếp tục lấy độ dài từ B đến điểm tiếp theo trên đường tròn, cứ tiếp tục cho đến khi bạn có được 6 điểm đánh dấu A, B, C, D, E, F trên đường tròn.
• Bước 5: Nối các điểm lại với nhau để tạo thành hình lục giác đều.

2. Sử dụng Thước Kẻ và Ê Kê

• Bước 1: Vẽ một cạnh đầu tiên (AB) với độ dài mong muốn.
• Bước 2: Đặt ê kề sao cho góc giữa cạnh vừa vẽ và cạnh tiếp theo là \(120^\circ\).
• Bước 3: Vẽ từng cạnh tiếp theo cho đến khi tạo thành hình lục giác.

Lời Kết

Hình lục giác đều không chỉ đơn thuần là một khái niệm trong toán học mà còn là một hình dạng tự nhiên tồn tại trong nhiều lĩnh vực khác nhau, từ kiến trúc cho đến công nghệ và nghệ thuật. Với các đặc điểm nổi bật như tính đối xứng và khả năng ứng dụng linh hoạt, lục giác đều mang lại nhiều giá trị mà chúng ta có thể khám phá và áp dụng. Hy vọng rằng bài viết này đã cung cấp cho bạn cái nhìn sâu sắc về hình lục giác đều, từ những định nghĩa cơ bản, công thức tính toán đến những ứng dụng thực tế trong đời sống. Nếu bạn có bất kỳ thắc mắc nào về hình học hoặc muốn tìm hiểu thêm về hình dạng này, đừng ngần ngại chia sẻ để cùng nhau thảo luận nhé!